
- #Projectile motion calculator unknown initial height how to
- #Projectile motion calculator unknown initial height professional
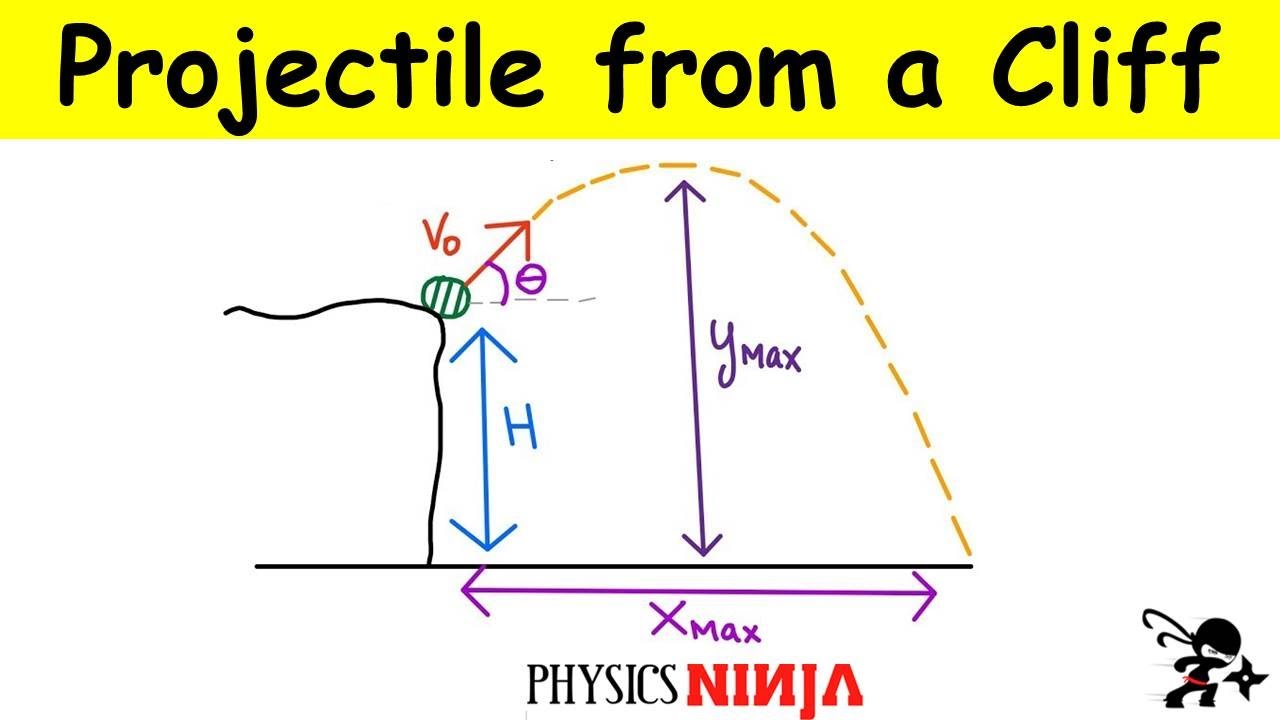
Maybe there's this nastyĬraggy cliff bottom here that you can't fall on. Run in order to avoid maybe the rocky shore right here that you might want to avoid. This cliff high and this speed how fast do I have to
#Projectile motion calculator unknown initial height professional
And if you were a cliff diver, I mean don't try this at home, but if you were a professional cliff diver you might want to know for Question you might get asked: how far did this person go horizontally before striking the water? This is a classic problem, They initially went this way, and they start to fall down, and they do something like pschhh, and then they splash in the water, hopefully they don't hitĪny boats or fish down here. They fly through the air, there's water down here, so And let's say they're completely crazy, let's say this cliff is 30 meters tall. Let's say they run off of this cliff with five meters per second of initial velocity, They're gonna run but theyĭon't jump off the cliff, they just run straight off of the cliff 'cause they're kind of nervous. "whoa, let's do this." We're gonna do this, they're pumped up.
Gonna cliff dive or base jump, and they're gonna be like The object for a projectile is completely horizontal, then that object is a horizontally launched projectile. Has to start off with, if the table's flat and horizontal, the velocity of the ball initially If you just roll theīall off of the table, then the velocity the ball What could that be? I mean a boring example, it's just a ball rolling off of a table. Off of a cliff, let's say, in this straight horizontal direction with no vertical component to start with, then it's a horizontally Launched projectile is any object that gets launched in a completely horizontal What that is in a minute so that you don't fall into the same trap. There is nothing new, except that there's oneĪspect of these problems that people get stumpedīy all of the time.
#Projectile motion calculator unknown initial height how to
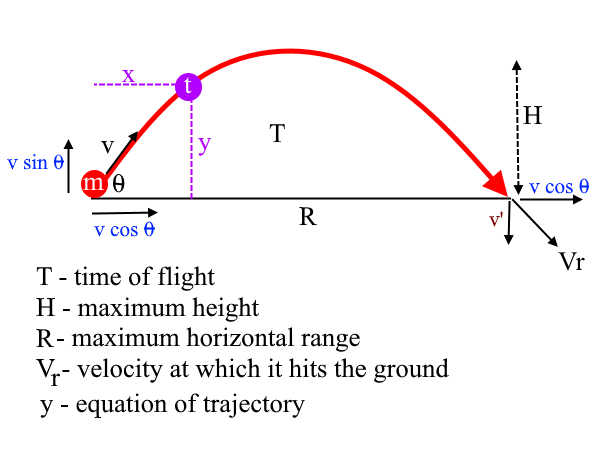
If you already know how to do projectile problems, Talk about how to handle a horizontally launched Hope this helps! (Yes, I am the slightest bit too lazy to actually write the symbol for theta) We can write this as:Īnd there you have both the magnitude and angle of the final velocity. To find the angle, you would need to do some trig and realize that the angle from the horizontal is opposite to Vfy and adjacent to Vfx. That's the magnitude of the final velocity. The components will be the legs, and the total final velocity will be the hypotenuse. Now that you have the final velocity components, you can set up a right triangle to solve for the combined final velocity. You could then use the time-independent formula: You have vertical displacement (30 m), acceleration (9.8 m/s^2), and initial velocity (0 m/s). To find the vertical final velocity, you would use a kinematic equation. Horizontal is easy, there is no horizontal acceleration, so the final velocity is the same as initial velocity (5 m/s). Attribution: Cmglee, CC BY-SA 3.0, via Wikimedia Commons.If you were asked to find final velocity, you would need both the vertical and horizontal components of final velocity. Trajectories of projectiles launched at different elevation angles but at the same speed (g = 10 m/s²). If you've used the trigonometric functions calculator, you know that sin(2 x) = 2sin( x)cos( x), so we can write the final formula as: Velocity, in our case, is the horizontal velocity V x = V₀ × cos(α), and the time to reach the ground is a value we've already calculated:ĭ = V × t = V₀ × cos( α) × 2 × V₀ × sin( α)/ g The projectile range is the distance traveled by the object when it returns to the ground (so y = 0):įrom that equation, we'll find t, which is the time of flight to the ground:Īlso, we know that we can find the maximum distance of the projectile from the widely known formula: d = V × t (learn more in our distance calculator). To find the formula for the projectile range, let's start with the equation of motion. Launch from the ground (initial height = 0) Let's split the equations into two cases: when we launch the projectile from the ground and when the object is thrown from some initial height (e.g., table, building, bridge).ġ.


 0 kommentar(er)
0 kommentar(er)
